In this year’s Glorney, Gilbert, Robinson, and Stokes Cups, held in Paisley, Scotland, all games from rounds 1-3 were available on live boards, but there was a delay for rounds 4 and 5. The organisers have now made the remaing games available, and all Irish games are now available in the games archive here (and on the ICU web site).
One game that caught the eye was the 125-move marathon in the last round of the Robinson Cup, between Daniel Kutchoukov (Netherlands) and Adam Murphy (Ireland).
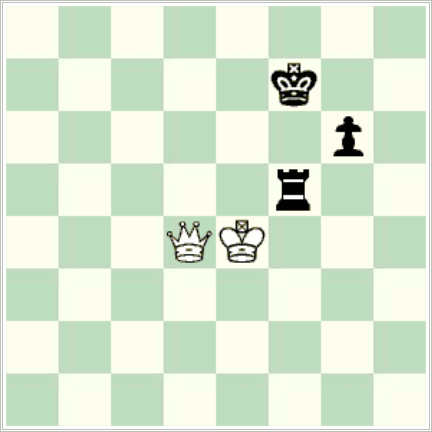
82… ?
What would you play as Black here?
I think I can honestly say that I would play 82… Kg8 without hesitation, at any time limit, on the basis that Black has a fortress and there’s no way for White to make progress. That was my instant reaction on first seeing the game.
This is one of those cases where a little learning is not a dangerous thing. The defence is actually a bit more complicated than that, and it all gets much more difficult if Black doesn’t maintain the fortress. But 82… Kg8 is indeed correct (the only other move to draw is 82… Rf6) and preserving the fortress greatly simplifies the defence, leaving only one way to go wrong later.
By far the best way to follow this is via the Nalimov tablebases. The arrow keys move the position up, down, or sideways, and are useful to see how the evaluation and best continuations vary. Typing ‘b’ repeatedly plays the best move for each side.
With 82… Kg8, the idea is to keep the king on one of the four corner squares, with the rook permanently posted on f5, keeping out the white king.
The reason it’s not so simple is that after 83. Qd8+ Kg7 84. Qh4, the reply 84… Kg8? loses after 85. Qh6! Kf7 86. Qh7+! Kf6 87. Qg8. After 87… Re5+ 88. Kd4 Rf5 89. Qf8+ Kg5 90. Qg7 Kh5 91. Ke4 Kg5 92. Qh8, something must give way. Though even here the subsequent continuation requires some involved manoeuvring. So (after 83. Qd8+ Kg7 84. Qh4) the rook has to move. Is it more important to cover the rank or the file? This is not so obvious. It turns out that it’s important to cover the f-file: the only moves that draw are 84… Rf8, 84… Rf7, 84… Rf6, and 84… Rf1. That’s certainly missable (since 84… Rh5 is very plausible); but once Black gets that right and otherwise hugs the corner, he can’t go wrong.
In the game, from the diagram, Adam Murphy played the natural, but wrong, 82… Rh5?. After 83. Qd7+ Kf6, White could have won via 84. Kd4 Rf5 85. Qh7 Rh5 (85… Kg5 86. Ke4 reaches the line above) 86. Qg8 Rh4+ (lasts the longest; 86… Rf5 87. Qf8+ Kg5 88. Qg7) 87. Kd5 and the White king maneouvres around to f8. Instead after 84. Qd8+ Kf7 White in turn erred with the (very natural) 85. Kf4? when it’s once again a draw with best play.
There are several more twists and turns according to the tablebases, though what constitutes best play is mysterious in many cases. In what follows, ‘!’ means the only move that preserves the best-play result, and ‘?’ indicates a move that changes the result with best play: 85… Rf5+ 86. Kg4 Rh5 (86… Kg7=) 87. Qd4 Rf5 88. Qd7+ Kf6? (again this insistence on moving forward! 88… Kg8!=) 89. Qh7 Rg5+ 90. Kf4? (90. Kf3!+- (mysterious)) 90… Rf5+? (90… Rh5!=) 91. Ke4 Re5+ 92. Kd4 Rh5 93. Qg8 Rh4+ 94. Kd5 Rh5+ 95. Kd6 Rf5 96. Qd8+? (allowing the fortress again; 96. Qh8+ is quickest) 96… Kg7 97. Ke6 Kh6? (and yet again … Black just had the wrong idea; 97… Kh7= is the fortress) 98. Qh4+? (returning the favour; 98. Qh8+ and 98. Qg8 win) 98… Kg7! 99. Qe7+ Kh6 (still drawn, but 99… Kg8 or 99… Kh8 are simpler) 100. Qd8 Kh5? (no! 100… Kg7 and 100… Kh7 are the only moves that draw) 101. Qh8+ Kg5 102. Qg7 Kh5 103. Qh7+ Kg5 104. Qh3 Rf6+ 105. Ke7 Rf5 106. Qh8 Kg4 107. Qh6 g5 108. Ke6? (and here is the final error: the unique move to win turns out to be 108. Qe6!, and if it’s obvious to you why this should be so, you must be a very good endgame player). The game was drawn in another 17 moves.
Reuben Fine describes Queen v. Rook and Pawn as ‘one of the most intricate endings that can come up’ (Basic Chess Endings (McKay, 1941), p. 562). Based on this game that seems apt; perhaps we could add that it seems significantly more tricky to win than to draw.
